Torej je preprosta obresti znesek, ki se plača za uporabo naloženega denarja za določeno obdobje. Po drugi strani pa, kadar obresti zapadejo v plačilo, se doda k glavnici, na katero se obračunajo obresti za naslednjo obdobje, kar se imenuje obrestne obresti . Torej, tukaj v tem članku boste našli osnovne razlike med navadnimi obrestmi in sestavljenimi obrestmi, ki smo jih sestavili po poglobljeni raziskavi dveh izrazov.
Primerjalna tabela
| Podlaga za primerjavo | Enostavno obresti | Obrestno obrestovanje |
|---|---|---|
| Pomen | Preprosti obresti se nanašajo na obresti, ki se izračunajo kot odstotek glavnice. | Obrestne obresti se nanašajo na obresti, ki se izračunajo kot odstotek glavnice in obračunane obresti. |
| Vrnitev | Manj | Primerjalno visoka |
| Glavni | Constant | Spreminja se med celotnim obdobjem zadolževanja. |
| Rast | Ostaja enakomerna | Hitro se poveča |
| Obresti od | Glavni | Glavni + skupne obresti |
| Formula | Enostavno obresti = P * r * n | Sestavljena obrestna mera = P * (1 + r) ^ nk |
Opredelitev enostavnih obresti
Enostavna obresti so obresti, ki se zaračunajo v odstotkih od prvotnega zneska posojenega ali glavnice, za celotno obdobje izposojanja. Obresti so cene, plačane za uporabo sredstev ali dohodkov, prejetih iz posojil. To je najlažja in najhitrejša metoda za izračun obresti na izposojeni ali izposojeni znesek. Najpogostejši primer navadnega obresti je posojilo za avto, kjer se obresti plačajo samo na prvotni znesek, ki ga posojilo ali izposodi. Za izračun zneska obresti se uporablja naslednja formula:
Formula : navadna obrestna mera = P × i × n
Kjer je P = glavni znesek
i = obrestna mera
n = število let
Na primer : Če si izposodite Rs. 1000 od tvojega prijatelja @ 10% na leto za 3 leta, potem moraš vrniti Rs.1300 svojemu prijatelju ob koncu tretjega leta Rs 1000 za glavnico in Rs. 300 kot obresti, za ohranitev zneska s seboj. Če seštejemo glavnico in obresti, jo bomo imenovali Znesek. Ne smemo pozabiti na to, da je več denarja in obdobij, tem večji bo interes.
Opredelitev sestavljenih obresti
Obrestna obresti so obresti, ki se izračunajo kot odstotek popravljene glavnice, tj. Prvotne glavnice plus nabrane obresti iz preteklih obdobij. Pri tej metodi se seštejejo obresti iz prejšnjih let na začetno glavnico, s čimer se poveča znesek glavnice, na katero se obračunajo obresti za naslednje obdobje. Pri tem se obresti plačajo na glavnico in obresti, obračunane med trajanjem posojila.
Časovni interval med dvema obdobjema plačila obresti se imenuje Obdobje konverzije. Ob koncu obdobja preusmeritve se obresti povečajo kot:
| Obdobje konverzije | Sestavljen |
|---|---|
| 1 dan | Dnevno |
| 1 teden | Tedensko |
| 1 mesec | Mesečno |
| 3 mesece | Četrtletno |
| 6 mesecev | Polletno |
| 12 mesecev | Letno |
Običajno banke plačujejo obresti na polletni osnovi, toda finančne institucije imajo politiko plačevanja obresti četrtletno. Za izračun obrestnih obresti morate uporabiti to formulo:
Formula : sestavljena obrestna mera = P {(1 + i) n - 1}
Kje, P = glavni
n = število let
i = obrestna mera na obdobje
Ključne razlike med navadnimi obrestmi in sestavljenimi obrestmi
V nadaljevanju so glavne razlike med navadnimi obrestmi in obrestnimi obrestmi:
- Obresti, zaračunane na glavnico za celotno obdobje posojila, se imenujejo navadne obresti. Obresti, izračunane na podlagi glavnice in predhodno pridobljenih obresti, se imenujejo sestavljena obresti.
- Komponentne obresti dajejo visoko donosnost v primerjavi z navadnimi obrestmi.
- V enostavnih obrestih glavnica ostane nespremenjena, v primeru sestavljenih obresti pa se glavnica zaradi učinka pripojitve spremeni.
- Stopnja rasti enostavnih obresti je nižja od obrestne obresti.
- Izračun preproste obresti je preprost, izračun sestavljenih obresti pa je zapleten.
Video: Simple Vs Compound obresti
Primer
Recimo, da je Alex položil Rs. 1000 bankam pri 5-odstotni obrestni meri (preprosta in sestavljena) za 3 leta. Ugotovite, kakšen je skupni interes, ki ga bo dobil ob koncu tretjega leta?
Rešitev : Tukaj P = 1000, r = 5% in t = 3 leta
Enostavno zanimanje =

Sestavljena obresti =
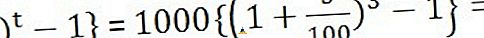
Zaključek
Obresti so pristojbine za uporabo tujih denarnih sredstev. Obstaja veliko razlogov za plačilo obresti, kot so časovna vrednost denarja, inflacija, oportunitetni stroški in dejavnik tveganja. Preprosta obrestna mera se hitro izračuna, vendar je obrestna obrestna mera praktično težka. Če izračunate tako navadne obresti kot obrestne obresti za določeno glavnico, obrestno mero in čas, boste vedno ugotovili, da je obrestna obrestna mera vedno višja od navadne obresti zaradi učinka združevanja.