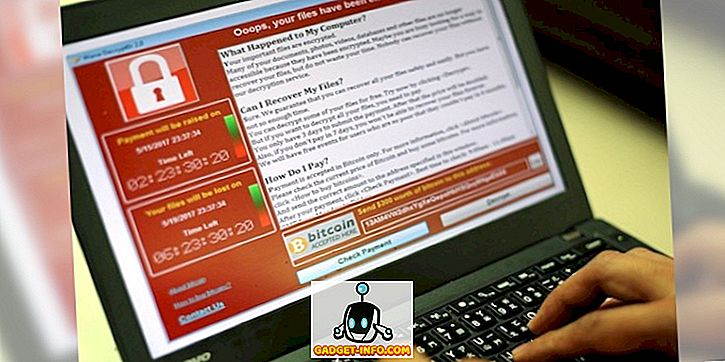
Če zaporedje sledi določenemu pravilu, se imenuje napredovanje. To ni popolnoma enako seriji, ki je definirana kot seštevek elementov zaporedja. Preberite si članek in se pozanimajte o pomembni razliki med zaporedjem in serijo.
Primerjalna tabela
| Podlaga za primerjavo | Zaporedje | Serija |
|---|---|---|
| Pomen | Zaporedje je opisano kot niz številk ali predmetov, ki sledi določenemu vzorcu. | Serija se nanaša na vsoto elementov zaporedja. |
| Naročilo | Pomembno | Včasih je pomembno |
| Primer | 1, 3, 5, 7, 9, 11 .... | 1 + 3 + 5 + 9 + 11 ... |
Opredelitev zaporedja
V matematiki je urejen niz predmetov ali številk, kot je 1, 2, 3, 4, 5, 6, … in n…. rečeno, da so v zaporedju, če ima po določenem pravilu določeno vrednost. Člani sekvence se imenujejo izraz ali element, ki je enak kakršni koli vrednosti naravnega števila. Vsak izraz v zaporedju je povezan s prejšnjim in naslednjim izrazom. Na splošno imajo zaporedja skrita pravila ali vzorec, ki vam pomaga ugotoviti vrednost naslednjega termina.
N-ti izraz je funkcija celega števila n (pozitivno), ki se obravnava kot splošni izraz zaporedja. Zaporedje je lahko končno ali neskončno.
- Končna zaporedje : Končno zaporedje je tisto, ki se ustavi na koncu seznama števil 1, 2, 3, 4, 5, 6, … a n, predstavlja:

- Neskončno zaporedje : neskončno zaporedje se nanaša na zaporedje, ki je neskončno, 1, 2, 3, 4, 5, 6, … a n…., predstavlja:

Opredelitev serije
Dodatek izrazov zaporedja (a n ) je znan kot serija. Tako kot zaporedje je lahko tudi serija končna ali neskončna, kjer je končna serija tista, ki ima končno število izrazov zapisanih kot 1 + a 2 + a 3 + a 4 + a 5 + a 6 + …… a n . Za razliko od neskončnih serij, kjer število elementov ni končno ali je neskončno, je zapisano kot 1 + a 2 + a 3 + a 4 + a 5 + a 6 + …… a n + ….
Če a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + …… a n = S n, se S n šteje kot vsota za n elementov serije. Vsota izrazov je pogosto predstavljena z grško črko sigma (Ʃ). Zato

Ključne razlike med zaporedjem in serijami
Razliko med zaporedjem in serijo je mogoče jasno sestaviti iz naslednjih razlogov:
- Zaporedje je definirano kot zbirka števil ali predmetov, ki sledijo določenemu vzorcu. Ko se elementi zaporedja seštejejo, so ti znani kot serije.
- Red je pomemben v zaporedju, saj obstaja določeno pravilo, ki predpisuje vzorec zaporedja. Zato je 1, 2, 3 trije drugačen od 3, 1, 2. Po drugi strani pa lahko v zaporedju vrstnega reda videza ali pa ne bo pomembno, kot v primeru absolutno konvergentnega niza, da red ni pomemben. Torej, 1 + 2 + 3 je enako kot 3 + 1 + 2, samo njihovo zaporedje je drugačno.
Zaključek
Aritmetična progresija (AP) in geometrijska progresija (GP) sta tudi zaporedja, ne serija. Aritmetična progresija je zaporedje, v katerem je skupna razlika med zaporednimi izrazi, kot so 2, 4, 6, 8 itd. Nasprotno, v geometrijskem napredovanju je vsak element zaporedja skupni večkratnik prejšnjega izraza, kot so 3, 9, 27, 81 in tako naprej. Podobno je Fibonaccijeva zaporedje tudi ena od priljubljenih neskončnih zaporedij, v katerih je vsak izraz dobljen z zbiranjem dveh predhodnih izrazov 1, 1, 3, 5, 8, 13, 21 in tako naprej.