V nasprotju s tem v primeru kombinacije naročilo sploh ni pomembno. Ne samo v matematiki, temveč tudi v praktičnem življenju, skozi ta dva koncepta redno gremo. Čeprav tega nikoli ne opazimo. Torej pozorno preberite članek, da veste, kako sta ti dve pojmi različni.
Primerjalna tabela
| Podlaga za primerjavo | Permutacija | Kombinacija |
|---|---|---|
| Pomen | Permutacija se nanaša na različne načine urejanja niza predmetov v zaporednem vrstnem redu. | Kombinacija se nanaša na več načinov izbire predmetov iz velikega števila predmetov, tako da njihov vrstni red ni pomemben. |
| Naročilo | Pomembno | Nepomemben |
| Označuje | Dogovor | Izbira |
| Kaj je to? | Naročeni elementi | Neurejeni nizi |
| Odgovori | Koliko različnih ureditev lahko ustvarite iz danega niza predmetov? | Koliko različnih skupin lahko izberemo iz večje skupine predmetov? |
| Izpeljava | Večkratna permutacija iz ene kombinacije. | Posamezna kombinacija iz ene permutacije. |
Opredelitev permutacije
Permutacijo definiramo kot različne načine urejanja nekaterih ali vseh članov niza v določenem vrstnem redu. Vključuje vse možne ureditve ali prerazporeditve danega niza v razločevalni vrstni red.
Na primer: Vse možne permutacije, ustvarjene s črkami x, y, z -
- Če vzamemo vse tri hkrati, so xyz, xzy, yxz, yzx, zxy, zyx.
- Če vzamemo dve hkrati, sta xy, xz, yx, yz, zx, zy.
Skupno število možnih permutacij n stvari, vzetih r naenkrat, se lahko izračuna kot:
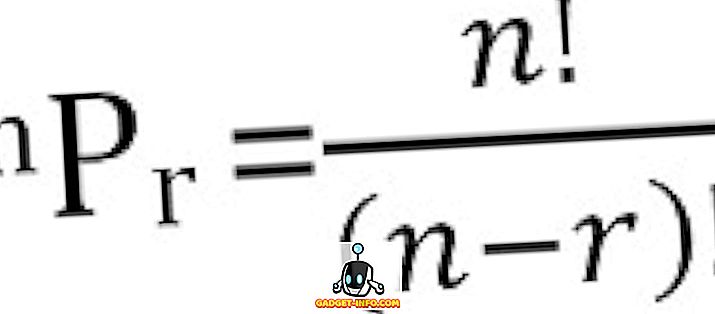
Opredelitev kombinacije
Kombinacija je definirana kot različni načini izbire skupine, tako da se nekateri ali vsi člani skupine sprejmejo brez naslednjega vrstnega reda.
Na primer: Vse možne kombinacije, izbrane s črko m, n, o -
- Če želite izbrati tri od treh črk, je edina kombinacija mno
- Če želite izbrati dve od treh črk, so možne kombinacije mn, no, om.
Skupno število možnih kombinacij n stvari, ki smo jih vzeli r naenkrat, lahko izračunamo kot:
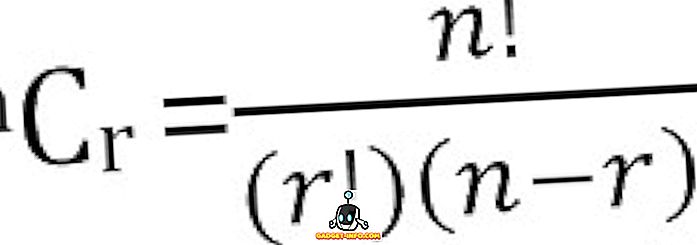
Ključne razlike med permutacijo in kombinacijo
Razlike med permutacijo in kombinacijo so jasno sestavljene iz naslednjih razlogov:
- Izraz permutacija se nanaša na več načinov urejanja niza predmetov v zaporednem vrstnem redu. Kombinacija pomeni več načinov izbire predmetov iz velikega nabora predmetov, tako da je njihov vrstni red nepomemben.
- Primarna razlikovalna točka med tema dvema matematičnima konceptoma je vrstni red, umeščenost in položaj, tj. V zgoraj navedenih permutacijskih lastnostih je pomembna, kar pa v primeru kombinacije ni pomembno.
- Permutation pomeni več načinov za ureditev stvari, ljudi, številk, abeced, barv itd. Po drugi strani kombinacija označuje različne načine izbire elementov menija, hrane, oblačil, predmetov itd.
- Permutacija ni nič drugega kot urejena kombinacija, medtem ko kombinacija pomeni neurejene nize ali združevanje vrednosti znotraj določenih kriterijev.
- Številne permutacije se lahko izpeljejo iz ene same kombinacije. Nasprotno pa lahko iz ene permutacije dobimo samo eno kombinacijo.
- Odgovori o permutacijah Koliko različnih ureditev lahko ustvarite iz danega niza predmetov? V nasprotju s kombinacijo, ki pojasnjuje, koliko različnih skupin je mogoče izbrati iz večje skupine predmetov?
Primer
Recimo, da obstaja situacija, ko morate ugotoviti skupno število možnih vzorcev dveh od treh objektov A, B, C. V tem vprašanju morate najprej razumeti, ali je vprašanje povezano s permutacijo ali kombinacija in edini način, da to ugotovite, je, da preverite, ali je naročilo pomembno ali ne.
Če je vrstni red pomemben, je vprašanje povezano s permutacijo, možni vzorci pa so AB, BA, BC, CB, AC, CA. Kjer se AB razlikuje od BA, se BC razlikuje od CB in AC je različna CA.
Če je naročilo nepomembno, je vprašanje povezano s kombinacijo, možni vzorci pa so AB, BC in CA.
Zaključek
Z zgornjo razpravo je jasno, da so permutacija in kombinacija različni izrazi, ki se uporabljajo v matematiki, statistiki, raziskavah in našem vsakodnevnem življenju. Pomembno je vedeti, da je glede teh dveh pojmov permutacija za dani niz objektov vedno višja od njene kombinacije.