Idealno merilo osrednje težnje je tisto, ki je jasno opredeljeno, lahko razumljivo, preprosto izračunljivo. Temeljiti mora na vseh opazovanjih, najmanj pa na ekstremnih opazovanjih v nizu podatkov.
Ljudje pogosto nasprotujejo ta dva ukrepa, vendar je dejstvo, da so različni. Ta članek posebej izpostavlja osnovne razlike med srednjo in srednjo vrednostjo. Poglej.
Primerjalna tabela
| Podlaga za primerjavo | Pomeni | Mediana |
|---|---|---|
| Pomen | Srednja se nanaša na preprosto povprečje danega niza vrednosti ali količin. | Mediana je definirana kot srednja številka v urejenem seznamu vrednosti. |
| Kaj je to? | To je aritmetično povprečje. | To je pozicijsko povprečje. |
| Predstavlja | Težišče podatkovnega niza | Težišče podatkovnega niza Srednja točka nabora podatkov |
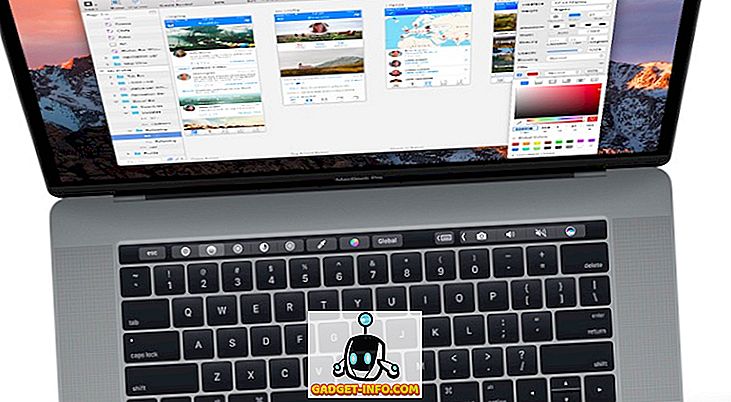
| Uporabnost. \ T | Normalna porazdelitev | Izkrivljena porazdelitev |
| Outliers | Srednja je občutljiva na ekstremne vrednosti. | Mediana ni občutljiva na outliers. |
| Izračun | Srednja vrednost se izračuna tako, da se seštevajo vsa opažanja in nato dobljena vrednost deli s številom opazovanj. | Za izračun mediane je niz podatkov razvrščen v naraščajočem ali padajočem zaporedju, potem je vrednost, ki pade v točno sredino novega niza podatkov, mediana. |
Opredelitev srednje vrednosti
Srednja vrednost je široko uporabljena mera centralne tendence, ki je opredeljena kot povprečje množice vrednosti. Predstavlja model in najpogostejšo vrednost danega razpona vrednosti. Lahko se izračuna tako v diskretni kot v kontinuirani seriji.
Srednja vrednost je enaka vsoti vseh opazovanj, deljeno s številom opazovanj v nizu podatkov. Če je vrednost, ki jo predpostavlja spremenljivka, enaka, bo tudi njena srednja vrednost enaka. Povprečje je lahko dveh vrst, povprečje vzorca (x̅) in povprečna populacija (µ). Lahko se izračuna z dano formulo:
- Aritmetična sredina :

n = število vrednosti - Za diskretne serije :

- Za kontinuirane servise :

A = Predpostavljeno povprečje
C = skupni delitelj
Opredelitev mediane
Mediana je še eno pomembno merilo osrednje težnje, ki se uporablja za porazdelitev vrednosti v dva enaka dela, tj. Večjo polovico vzorca, populacijo ali porazdelitev verjetnosti iz spodnje polovice. To je srednja vrednost, ki se doseže, ko so opažanja razvrščena v določenem vrstnem redu, bodisi naraščajoče ali padajoče.
Za izračun mediane najprej pripišite opazovanja v najnižji do najvišji ali najvišji do najnižje vrednosti, nato pa uporabite ustrezno formulo, kot je navedeno v spodnjih pogojih:
- Če je število opazovanj čudno :

- Če je število opazovanj celo :

- Za zvezne serije :

c = skupna pogostnost predhodnega srednjega razreda
f = pogostnost srednjega razreda
h = širina razreda
Ključne razlike med srednjimi in mediano
Pomembne razlike med srednjo in srednjo vrednostjo so navedene v spodnjem članku:
- V statistiki je povprečje definirano kot preprosto povprečje danega niza vrednosti ali količin. Mediana je srednja številka urejenega seznama vrednosti.
- Medtem ko je srednja vrednost aritmetična sredina, je mediana pozicijsko povprečje, v bistvu položaj podatkovnega niza določa vrednost mediane.
- Srednje označuje težišče podatkovnega niza, medtem ko mediana poudarja srednjo vrednost podatkovnega niza.
- Srednja vrednost je primerna za normalno porazdeljene podatke. Na drugi strani je mediana najboljša, kadar je distribucija podatkov izkrivljena.
- Srednja vrednost je močno prizadeta zaradi skrajne vrednosti, ki ni v primeru mediane.
- Srednja vrednost se izračuna tako, da se seštevajo vsa opažanja in nato dobljena vrednost deli s številom opazovanj; rezultat je povprečen. V nasprotju s srednjo vrednostjo je niz podatkov razvrščen v naraščajočem ali padajočem zaporedju, potem je vrednost, ki pade v točno sredino novega podatkovnega niza, mediana.
Primer
Poišči srednjo vrednost in mediano danega niza podatkov:
58, 26, 65, 34, 78, 44, 96
Rešitev: Za izračun pomeni, da morate vsoto opazovanj razdeliti s številom opazovanj,

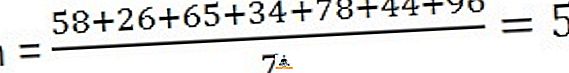
Za izračun mediane najprej uredite niz v zaporedju, tj. Najnižje do najvišje,
26, 34, 44, 58, 65, 78, 96
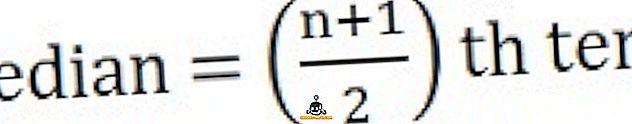
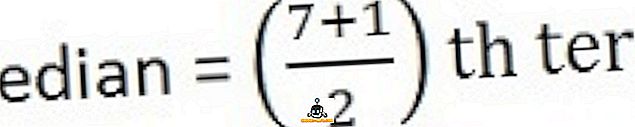
Zaključek
Po pregledu zgornjih točk lahko rečemo, da sta ti dve matematični pojmi različni. Aritmetična sredina ali povprečje se šteje za najboljšo merilo centralne tendence, saj vsebuje vse značilnosti idealne mere, vendar ima eno pomanjkljivost, da nihanja vzorčenja vplivajo na povprečje.
Na enak način je tudi mediana nedvoumno definirana in lahko razumljiva in izračunana, najboljša stvar pri tem ukrepu pa je, da nanj ne vplivajo vzorčna nihanja, vendar je edina slabost mediane, da ne temelji na vseh opažanja. Za klasifikacijo odprtega konca je mediana običajno prednost pred povprečjem.