Razvrščanje je osnovna operacija, v kateri so elementi matrike razvrščeni v nekakšnem specifičnem vrstnem redu, da bi povečali možnost iskanja. S preprostimi besedami so podatki razvrščeni tako, da jih je mogoče enostavno iskati.
Primerjalna tabela
| Podlaga za primerjavo | Vstavljanje Razvrsti | Razvrščanje izbire |
|---|---|---|
| Osnovno | Podatki so razvrščeni z vstavljanjem podatkov v obstoječo sortirano datoteko. | Podatki so razvrščeni z izbiro in postavitvijo zaporednih elementov na razvrščeno lokacijo. |
| Narava | Stabilno | Nestabilno |
| Postopek, ki ga je treba upoštevati | Elementi so vnaprej znani, medtem ko je lokacija za njihovo iskanje. | Lokacija je že znana, medtem ko se elementi iščejo. |
| Takojšnji podatki | Insertion sort je tehnika sortiranja v živo, ki lahko obravnava takojšnje podatke. | Ne more obravnavati takojšnjih podatkov, biti mora prisoten na začetku. |
| Najboljša kompleksnost primera | O (n) | O (n 2 ) |
Opredelitev vrste vstavljanja
Vstavljanje razvrsti deluje tako, da v obstoječo sortirano datoteko vstavi niz vrednosti. Razvrščeno matriko konstruira tako, da vstavi posamezen element naenkrat. Ta postopek se nadaljuje, dokler ni celotno polje razvrščeno v nekem vrstnem redu. Primarni koncept vstavljanja je, da se vsak element vstavi na ustrezno mesto na končnem seznamu. Metoda razvrščanja z vstavljanjem shrani učinkovito količino pomnilnika.
Delo vrste Vstavljanje
- Uporablja dva niza nizov, kjer shranjujejo razvrščene podatke in druge na nesortirane podatke.
- Algoritem za razvrščanje deluje, dokler v nesortiranem nizu ni elementov.
- Predpostavimo, da so v matriki elementi 'n' števila. Sprva element v indeksu 0 (LB = 0) obstaja v razvrščenem nizu. Preostali elementi so v nesortirani particiji seznama.
- Prvi element nesortiranega dela ima indeks indeksa 1 (če je LB = 0).
- Po vsaki ponovitvi izbere prvi element nesortirane particije in ga vstavi v ustrezno mesto v razporejenem nizu.
Prednosti vrste vstavljanja
- Enostavna izvedba in zelo učinkovita uporaba pri majhnih nizih podatkov.
- Dodatna zahteva pomnilniškega prostora za sortiranje vstavljanja je manjša (tj. O (1)).
- Šteje se, da je tehnika razvrščanja v živo, saj je seznam mogoče razvrstiti po prejemu novih elementov.
- Je hitrejši od drugih algoritmov za razvrščanje.
Primer:
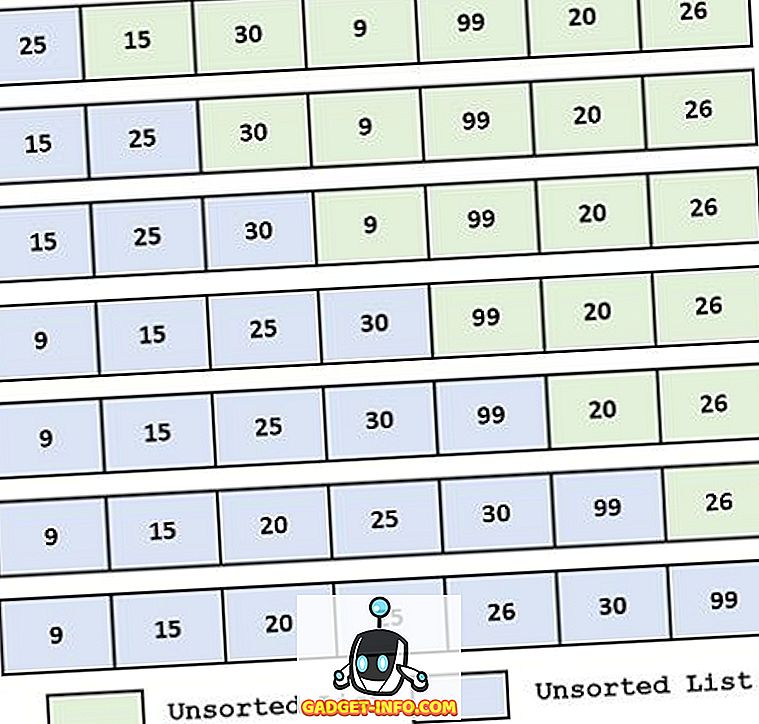
Opredelitev sortne vrste
Selekcija sortiranja opravi razvrščanje tako, da poišče najmanjšo vrednost in jo vnese v prvo ali zadnjo pozicijo v skladu z naročilom (naraščajoče ali padajoče). Postopek iskanja minimalnega ključa in njegovo postavitev v pravilen položaj se nadaljuje, dokler se vsi elementi ne postavijo na pravi položaj.
Delovanje sortne vrste
- Predpostavimo polje ARR z N elementi v pomnilniku.
- Pri prvem prehodu se poišče najmanjši ključ skupaj z njegovim položajem, nato pa se ARR [POS] zamenja z ARR [0]. Zato je ARR [0] razvrščeno.
- V drugem prehodu se ponovno določi položaj najmanjše vrednosti v podpodročju elementov N-1. Zamenjajte ARR [POS] z ARR [1].
- V prelazu N-1 se izvede isti postopek za razvrščanje števila N elementov.
Primer:
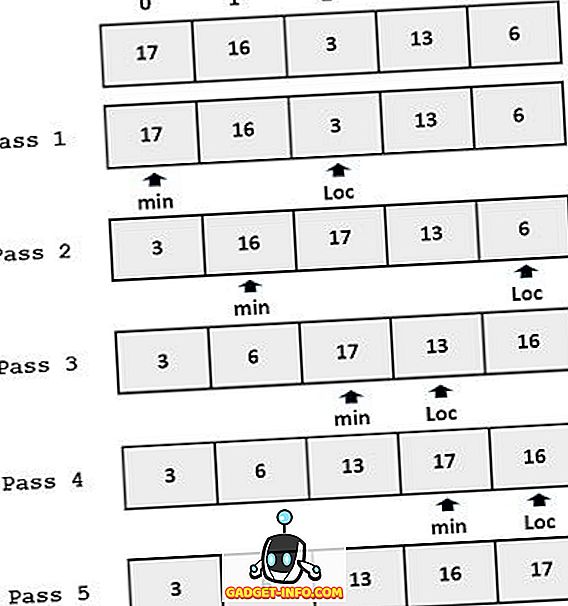
Ključne razlike med vrstami za vstavljanje in sortiranjem
- Vrsta vstavljanja običajno izvede operacijo vstavljanja. Nasprotno, izbirna vrsta izvede izbiro in pozicioniranje zahtevanih elementov.
- Razvrščanje vstavljanja naj bi bilo stabilno, medtem ko vrsta razvrščanja ni stabilen algoritem.
- V vstavitvenem algoritmu razvrščanja so elementi predhodno znani. Nasprotno pa izbirna vrsta vnaprej vsebuje lokacijo.
- Vstavljanje razvrščanja je tehnika razvrščanja v živo, kjer se prispeli elementi takoj razvrstijo na seznam, medtem ko sortna vrsta ne more dobro delovati z neposrednimi podatki.
- Sortiranje vstavljanja ima v najboljšem primeru čas delovanja O (n). V nasprotju s tem je najboljša časovna zahtevnost izbirne vrste O (n2).
Kompleksnost vrste vstavljanja
Najboljša zapletenost razvrščanja z vstavljanjem je O (n) -krat, tj. Ko je matrika predhodno razvrščena. Na enak način, ko je polje razvrščeno v obratnem vrstnem redu, se prvi element nesortiranega niza primerja z vsakim elementom v razvrščenem nizu. Torej je v najslabšem primeru čas delovanja vrste Vstavljanje kvadratni, tj. O (n2) . V povprečnem primeru mora opraviti tudi minimalne (k-1) / 2 primerjave. Torej ima povprečni primer tudi kvadratni čas delovanja O (n2).
Kompleksnost izbora sort
Kot delo izbire, sortiranje ni odvisno od prvotnega vrstnega reda elementov v matriki, tako da ni veliko razlike med najboljšim in najslabšim primerom izbirne vrste.
Izbirna vrsta izbere element minimalne vrednosti, v izbirnem postopku se skenira vse 'n' število elementov; zato je v prvem prehodu opravljenih n-1 primerjav. Nato se elementi zamenjajo. Podobno v drugem prehodu tudi za iskanje drugega najmanjšega elementa zahtevamo skeniranje preostalih n-1 elementov in proces se nadaljuje, dokler ni celotno polje sortirano.
Tako je časovna kompleksnost izbirne vrste O (n2) .
= (n-1) + (n-2) + ……… .. + 2 + 1
= n (n-1) / 2 = O (n2)
Zaključek
Med obema algoritmoma razvrščanja je vrsta vstavljanja hitra, učinkovita, stabilna, medtem ko je vrsta razvrščanja učinkovita le, če je vključen majhen nabor elementov ali je seznam delno že razvrščen. Število primerjav, opravljenih z izbirno sorto, je večje od izvedenih premikov, medtem ko je pri razvrščanju vstavitve število premikov ali zamenjav elementov večje od primerjav.